Over Sudoku-Simpel.EU
Wil je meteen meer lezen over het oplossen van Sudoku? Gebruik dan het menu of de streepjes hierboven!
Sinds een aantal jaren ben ik een fanatiek Sudoku-oplosser. Ik begon met eenvoudige Sudoku’s en rommelde maar wat aan. Als ik niet verder kwam zocht ik op Google naar tips en trucs en vond die op vele verschillende, soms goed toegankelijke maar vaker ingewikkelde en/of anderstalige sites.
Na verloop van tijd kreeg ik het idee dat de meeste schrijvers van deze sites vergeten zijn hoe moeilijk het was om te beginnen, of misschien zijn ze wiskundig dermate goed onderlegd dat ze eenvoudigweg niet zien waar mensen zonder wiskundeknobbel tegenaan lopen. Zelf ben ik absoluut geen wiskundige en je hoeft ook zeker geen genie met cijfers te zijn om met veel plezier Sudoku’s op te lossen. Je merkt vanzelf tot welk niveau je het nog leuk vindt, maar het is jammer als je daarbij te snel afhaakt.
Toen ik pas begon met het oplossen van Sudoku’s bleef ik vaak hangen op een bepaald punt en keek dan ongestructureerd rond in de hoop dat me iets op zou vallen (wat ook regelmatig gebeurde, maar wat natuurlijk geen enkele garantie is dat je de puzzel tot een goed einde brengt).
Ik ontwikkelde een aantal systematische procedures die ervoor zorgen dat je geen oplossingen over het hoofd ziet, waardoor je veel moeilijkere Sudoku’s aankunt dan je zou verwachten. Sommige van deze procedures (zoals horizontaal en verticaal scannen) zullen ongetwijfeld al lang door anderen bedacht zijn, maar ik ben ze niet tegengekomen. De geavanceerde technieken die ik bespreek (X-wing, Y-wing) zijn algemeen bekend en het gebruik van scenario’s vond ik in eenvoudige vorm op een website.
Omdat ik het met mijn onderwijsachtergrond leuk vind om dingen uit te leggen aan anderen wil ik je via deze site helpen verkennen tot welk niveau je Sudoku’s oplossen leuk vindt.
Ik beschrijf een aantal basale technieken die je bij elke Sudoku kunt toepassen en eindig met technieken die alleen bij zeer moeilijke Sudoku’s nodig zijn. Bepaal gerust zelf welke tools je wilt gebruiken uit de gereedschapskist die ik je bied!
Mocht je tegen vragen aan lopen, een foutje zien, of suggesties voor verbetering hebben, laat het me dan a.u.b. weten via het contactformulier op deze site. Ik zal je zeker antwoorden.
Wat is een Sudoku?
Een Sudoku is een puzzel die bestaat uit een aantal hokjes (cellen) die een cijfer tussen 1 en 9 kunnen bevatten. In een onopgeloste Sudoku is een aantal cellen voor je ingevuld. Het oplossen van de Sudoku bestaat uit het zoeken en invullen van de juiste cijfers in de lege cellen. De puzzel is opgelost als alle velden zijn ingevuld.
Hoe ziet een Sudoku eruit?
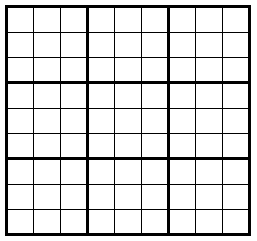
Een normale Sudoku heeft 9 rijen en 9 kolommen. Dit zijn dus in totaal 81 cellen. Deze cellen zijn verdeeld over 9 vierkante blokken van 9 velden (3 bij 3 telkens), zoals hier te zien is.
Waar moet je naartoe werken?
Een opgeloste Sudoku ziet er als volgt uit:
- op elke regel staan de cijfers 1 tot en met 9 precies één keer. De volgorde doet er niet toe,
- In elke kolom staan de cijfers 1 tot en met 9 precies één keer. De volgorde doet er niet toe,
- In elk blok staan de cijfers 1 tot en met 9 precies één keer. Ook hier doet de volgorde er niet toe.
Het is dus zaak te achterhalen welke cijfers er in de lege vakjes thuishoren. Elk vakje kent maar 1 correcte oplossing.
Naarmate de Sudoku moeilijker is, zijn er minder cijfers vooraf ingevuld en staan ze zo gegroepeerd dat een snelle oplossing zonder ‘trucs’ zo goed als onmogelijk lijkt. Verderop bespreek ik uitgebreid de technieken die je kunt toepassen om een schijnbaar onoplosbare Sudoku toch tot een goed einde te brengen.
Wat je moet onthouden
Eerst spreken we af hoe we de verschillende onderdelen van de Sudoku benoemen. De 9 regels noemen we van boven naar beneden R1 tot en met R9; de 9 kolommen noemen we van links naar rechts K1 tot en met K9 (sorry voor de puzzelaars uit andere landen, maar het Nederlandse woord voor kolom begint met een K); de blokken noemen we B1 tot en met B9 (van linksboven naar rechtsonder).
De cellen benoemen we door de het regelnummer en het kolomnummer weer te geven, bijvoorbeeld R2 K3 (de 3e cel van links op de 2e regel), of R9 K9 (de cel helemaal rechtsonder). Zie bijgaande figuur.

